Double Slit Experiment
With a single source of light, the distribution of light energy in the surrounding medium is uniform but when there are two adjacent sources of light giving out continuous waves of the same wavelength and amplitude and having the same phase or a constant difference in phase, the distribution of light energy is no longer uniform. At some points where the crest of one wave falls upon the crest of the other or trough of one falls upon the trough of the other, the resultant amplitude is increased and the energy becomes maximum, while at the other points where the crest of one wave falls upon the trough of the other and vice versa, the resultant amplitude is reduced to zero and the energy is minimum. This modification in the distribution of light energy obtained by the superposition of two or more waves is called interference of light.
The phenomenon of interference of light was first observed by Thomas Young (1773-1829). He successfully demonstrated it in 1802 and thus
established the wave character of light. The experiment can be explained by considering light to be a form of wave motion.
In Young's original experiment, a beam of sunlight was first allowed to pass ihrougn a pin-hole 5 (Fig. 10.5), into a darkened room. The beam was then allowed to pass, at a considerable distance away, through two pinholes Sr and placed symmetrically with respect to S. Here 5, and S2 are two coherent SQurces of the same intensity. The two sets of spherical waves coming out of these two pin holes interfered with each other in such a way as to form a symmetrical pattern of varying intensity on the screcn XY.
If the pin-holes be replaced by narrow slits and sunlight by monochromatic light, there will be cylindrical wavefronts in place of spherical wavefronts. A close examination t)f the light on the screen will show evenly spaced bright and dark fringes parallel to the length of the slit in the direction at right angles to SiS2 (Fig. 10.6). These fringes diminish in width as the distance 5; Si is increased until finally they disappear.
To get widely-spaced fringes the slits should be held quite close to each other. In the Young's experimental arrangement S is - 1 mm wide, 5;and S2 are at separation - 2 mm, the width of each slit being - 0.3 mm, The distance 55, is - 10 cm, 5,0 is ~ 2 metres.
To summarize the observations of Young's double slit experiment, one finds the following facts :
(a) If either, S, alone or S2 alone is open, the intensity of light is uniform on any plane like XY.
(b) If both 5, and S2 are open, the intensity alternately increases end decreases as one moves along XY, we say bright and dark fringes are seen.
(c) The fringe width (co) is proportional to the distance (D) between the slits and the screen and inversely proportional to the distance id) between the two slits 5, and S2 (Fig. 10.6).
established the wave character of light. The experiment can be explained by considering light to be a form of wave motion.
In Young's original experiment, a beam of sunlight was first allowed to pass ihrougn a pin-hole 5 (Fig. 10.5), into a darkened room. The beam was then allowed to pass, at a considerable distance away, through two pinholes Sr and placed symmetrically with respect to S. Here 5, and S2 are two coherent SQurces of the same intensity. The two sets of spherical waves coming out of these two pin holes interfered with each other in such a way as to form a symmetrical pattern of varying intensity on the screcn XY.
If the pin-holes be replaced by narrow slits and sunlight by monochromatic light, there will be cylindrical wavefronts in place of spherical wavefronts. A close examination t)f the light on the screen will show evenly spaced bright and dark fringes parallel to the length of the slit in the direction at right angles to SiS2 (Fig. 10.6). These fringes diminish in width as the distance 5; Si is increased until finally they disappear.
To get widely-spaced fringes the slits should be held quite close to each other. In the Young's experimental arrangement S is - 1 mm wide, 5;and S2 are at separation - 2 mm, the width of each slit being - 0.3 mm, The distance 55, is - 10 cm, 5,0 is ~ 2 metres.
To summarize the observations of Young's double slit experiment, one finds the following facts :
(a) If either, S, alone or S2 alone is open, the intensity of light is uniform on any plane like XY.
(b) If both 5, and S2 are open, the intensity alternately increases end decreases as one moves along XY, we say bright and dark fringes are seen.
(c) The fringe width (co) is proportional to the distance (D) between the slits and the screen and inversely proportional to the distance id) between the two slits 5, and S2 (Fig. 10.6).
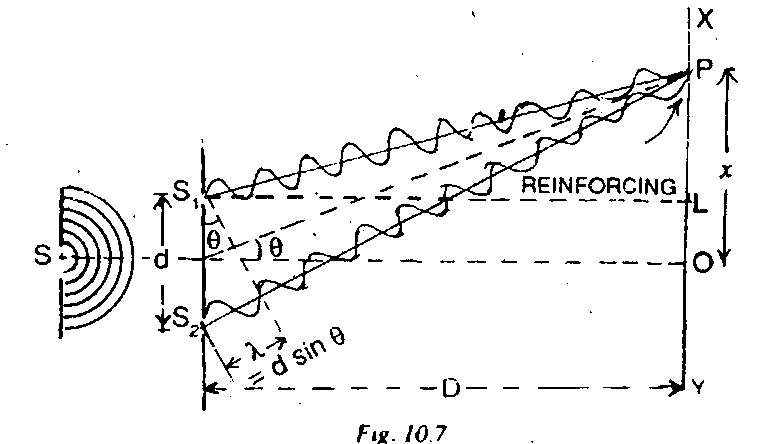
theory of Fringes. To explain the observations, let the source of mooo&hromatic light S emit waves (light) of wavelength X. As the spherical wavefronts of light proceeding from S reach, .9, and S2 (Fig. 10.7), each of them becomes a source of secondary wavefronts. Now S/ Wid S2 act as coherent sources of light. They have a constant phase difference and the secondary wavelets starting from them interfere in the space, The illumination at a point P on the screen XY will depend upon the path difference (j>) = (S2P—S^P) between the waves reaching P. Lei OP = X, ^ = d and the distance of the screen XY from S2 = D.
Evidently
$[t>--=(Sp + LP2yr2=\D2 + (x-d/2)2V>2 = D 1 + -x~d'1)
D2
Taking x to be small as compared with D, we expand the above by SinomLal theorem so that ■ *
2 D2 J 2D
Similarly, S,P = D 1 + 1 (x + d/2?] = D + l <*+d/2)2 L. 2 D J 2D
Calling p to be the path difference, we have. P = s2 p
= D + 1 ^ + [D + 1 (-y-^2)2|
2 D J 2 D J
= H- (x + df - [x - = -L axd\ 2D IA 21 \ 2> J 2D
P = ^ ... (0
D
(1) For maximum intensity at P, the path difference p should be equal to n X where n is an intcger.-
(2) For minimum intensity, p should be equal to (2n+ 1) X/2.
If a, and a2 arc the amplitudes of the disturbance at P due to St and S2 . separately, then with 5, and S2 together the amplitude at P will be maximum i.e. (ax +a2) if the path difference (p) is a whole number of wave lengths (X) and minimum i.e. (a, ~ a2) if p is an odd number of half wavelengths. Thus maxima should occur as follows :
p = id = n X for maxima where n = 0,1,2, 3,.... D
and p = = (2n + 1) — for minima where n = 0, 1,2,3,.... D 2
Thus if p = 0, IX, 2X, 3X...........wc get ccnircs of succcssivc bright
fringes on the scrccn. On the other hand, if p = X/2, 3X73. 5X/2...................
wc gel ccnircs of succcssivc dark fringes.
The separation of the succcssivc maxima gives the fringe width co. Thus
D , ,, , D , w = v>'*» =j(n+\)X--nX
or (o=^-X ...(H)
d
I like to share this Am Definition with you all through my article.
Wc had assumed that light had wave character and got the Conclusion thai tficrc should be bright and dark positions in the observation plane. Well, that is exactly what is observed experimentally. Wc also note the quantitative agreement between the experimental result and the equation
(if) that co<* D and « . The measurements of <y, d and D gives us d
A = ™5H ...0/0
D
It is notable that the interference experiments give us no information whether the waves arc longitudinal or transverse.
It is customary to express the wavelength of the visible ligK in Angstrom Unit (A), which is 10 wm. Thus for yellow light A = 6 x JO1 A. In the visible light the colors have the wavelength — Violet ~ 4000 'A, Green ~ 5600 A, Yellow - 5900 A, Red ~ 7500 A. But the light of X < 4000 A, which is not visible to the eye is called ultraviolet ; and the light of A >75'K) A, which again is invisible, is called infra-red. For lower in wavelength arc X-rays (a few A) and y-ravs (10 4 AY. far '..(gfor in wavelength arc microwaves ~ (10* ,4) ; and radiowaves ~ (H)'~ A). All these have essentially the same character, excepting the difference in the wavelength. Interference is shown by all these waves of'light.
Evidently
$[t>--=(Sp + LP2yr2=\D2 + (x-d/2)2V>2 = D 1 + -x~d'1)
D2
Taking x to be small as compared with D, we expand the above by SinomLal theorem so that ■ *
2 D2 J 2D
Similarly, S,P = D 1 + 1 (x + d/2?] = D + l <*+d/2)2 L. 2 D J 2D
Calling p to be the path difference, we have. P = s2 p
= D + 1 ^ + [D + 1 (-y-^2)2|
2 D J 2 D J
= H- (x + df - [x - = -L axd\ 2D IA 21 \ 2> J 2D
P = ^ ... (0
D
(1) For maximum intensity at P, the path difference p should be equal to n X where n is an intcger.-
(2) For minimum intensity, p should be equal to (2n+ 1) X/2.
If a, and a2 arc the amplitudes of the disturbance at P due to St and S2 . separately, then with 5, and S2 together the amplitude at P will be maximum i.e. (ax +a2) if the path difference (p) is a whole number of wave lengths (X) and minimum i.e. (a, ~ a2) if p is an odd number of half wavelengths. Thus maxima should occur as follows :
p = id = n X for maxima where n = 0,1,2, 3,.... D
and p = = (2n + 1) — for minima where n = 0, 1,2,3,.... D 2
Thus if p = 0, IX, 2X, 3X...........wc get ccnircs of succcssivc bright
fringes on the scrccn. On the other hand, if p = X/2, 3X73. 5X/2...................
wc gel ccnircs of succcssivc dark fringes.
The separation of the succcssivc maxima gives the fringe width co. Thus
D , ,, , D , w = v>'*» =j(n+\)X--nX
or (o=^-X ...(H)
d
I like to share this Am Definition with you all through my article.
Wc had assumed that light had wave character and got the Conclusion thai tficrc should be bright and dark positions in the observation plane. Well, that is exactly what is observed experimentally. Wc also note the quantitative agreement between the experimental result and the equation
(if) that co<* D and « . The measurements of <y, d and D gives us d
A = ™5H ...0/0
D
It is notable that the interference experiments give us no information whether the waves arc longitudinal or transverse.
It is customary to express the wavelength of the visible ligK in Angstrom Unit (A), which is 10 wm. Thus for yellow light A = 6 x JO1 A. In the visible light the colors have the wavelength — Violet ~ 4000 'A, Green ~ 5600 A, Yellow - 5900 A, Red ~ 7500 A. But the light of X < 4000 A, which is not visible to the eye is called ultraviolet ; and the light of A >75'K) A, which again is invisible, is called infra-red. For lower in wavelength arc X-rays (a few A) and y-ravs (10 4 AY. far '..(gfor in wavelength arc microwaves ~ (10* ,4) ; and radiowaves ~ (H)'~ A). All these have essentially the same character, excepting the difference in the wavelength. Interference is shown by all these waves of'light.